DIPS 4/2004 [tex source, PostScript, PDF file, dvi]
Author: A. Sergyeyev
We generalize earlier results of Fokas and Liu and find all
locally analytic (1+1)-dimensional evolution equations of order n that admit
an N-shock type solution with N< n+2.
To this end, we develop a refinement of the technique from our earlier work
(A. Sergyeyev, J. Phys. A: Math. Gen, 35 (2002), 7653-7660),
where
we completely characterized all (1+1)-dimensional evolution systems
 that are conditionally invariant under a given generalized
(Lie-Baecklund) vector field
that are conditionally invariant under a given generalized
(Lie-Baecklund) vector field 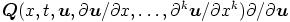 under the assumption that
the system of ODEs Q=0 is totally nondegenerate.
Every such conditionally invariant evolution system admits a reduction to a system of ODEs in t,
thus being a nonlinear counterpart to quasi-exactly solvable models in
quantum mechanics.
under the assumption that
the system of ODEs Q=0 is totally nondegenerate.
Every such conditionally invariant evolution system admits a reduction to a system of ODEs in t,
thus being a nonlinear counterpart to quasi-exactly solvable models in
quantum mechanics.
11 pages, AmS-LaTeX (LaTeX-2e).
To compile source files (.tex) one needs
the title page style files titlatex.tex.