DIPS 02/2002 [tex source, PostScript, PDF file, dvi]
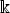 )
)Author: Arthemy V. Kiselev
Polynomials aj 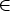
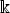 N[x], 1 <j<N, of degree deg aj = N are shown to be
closed w.r.t. action of the N-ary bracket [a1, ..., aN] = W(a1,...,aN ),
where W denotes the Wronskian determinant. This bracket is proved to
induce the homotopical N-Lie algebra structure on the polynomials
N[x], 1 <j<N, of degree deg aj = N are shown to be
closed w.r.t. action of the N-ary bracket [a1, ..., aN] = W(a1,...,aN ),
where W denotes the Wronskian determinant. This bracket is proved to
induce the homotopical N-Lie algebra structure on the polynomials 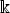 N[x] of
degree N, so that an extended Jacobi identity (with 2N-1 summands)
holds; the case N = 2 is the Lie bracket in sl2(
N[x] of
degree N, so that an extended Jacobi identity (with 2N-1 summands)
holds; the case N = 2 is the Lie bracket in sl2(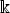 ) satisfying the Jacobi
identity.
) satisfying the Jacobi
identity.
The property of the Wronskian determinants to compose the homotopical
N-Lie algebras is proved to hold for arbitrary analytic functions aj The notion of the Wronskian determinant is generalized to the case of n
independent variables: (x1,...,xn)
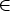
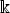 [[x]],
thus extending the former result. The identity [[
[[x]],
thus extending the former result. The identity [[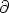 i1
i1  ...
...
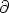 ik+1,
ik+1,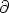 j1
j1  ...
...
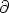 jl+1]]RN = 0 is discussed,
where
jl+1]]RN = 0 is discussed,
where 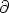 is a
derivation and [[.,.]]RN is the Richardson-Nijenhuis bracket.
is a
derivation and [[.,.]]RN is the Richardson-Nijenhuis bracket.
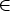
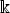 n, so that the resulting concept
preserves the homotopical N-Lie Jacobi identity.
n, so that the resulting concept
preserves the homotopical N-Lie Jacobi identity.
12 pages, LaTeX-2e (AmS-LaTeX).
To compile source files (.tex) one needs
the title page style files titlatex.tex.