Given a smooth manifold M, let V be a submanifold of the tangent bundle TM such that the projection of V to M is a submersion. To V is associated the space
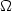 V of admissible curves, i.e. the curves
V of admissible curves, i.e. the curves 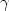 : [0,t
: [0,t ]
]  M whose velocities belong to
V . The boundary mapping
M whose velocities belong to
V . The boundary mapping 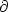 :
: 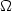 V
V  M×M sends a curve to its endpoints.
M×M sends a curve to its endpoints. 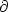 is
a smooth mapping; critical points of
is
a smooth mapping; critical points of 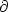 are V -geodesics. Special cases of
V -geodesics are (pseudo-)Riemannian geodesics (if V is the spherical
bundle of a (pseudo-)Riemannian structure), singular curves of vector
distributions (if V is a vector subbundle of TM), sub-Riemannian geodesics
e.t.c.
are V -geodesics. Special cases of
V -geodesics are (pseudo-)Riemannian geodesics (if V is the spherical
bundle of a (pseudo-)Riemannian structure), singular curves of vector
distributions (if V is a vector subbundle of TM), sub-Riemannian geodesics
e.t.c.Lagrange multipliers associated to all V -geodesics form a Lagrangian relation in the symplectic manifold T*M. Let
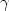 : [0,t]
: [0,t]  M be a V -geodesic and
M be a V -geodesic and
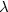
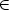 T *q(0)M be a correspondent Lagrange multiplier. An infinitesimal version
of the above Lagrangian relation is a Lagrangian subspace of the symplectic
space T
T *q(0)M be a correspondent Lagrange multiplier. An infinitesimal version
of the above Lagrangian relation is a Lagrangian subspace of the symplectic
space T (T*M). We associate to
(T*M). We associate to 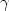 a one-parametric family of Lagrangian
subspaces (i.e. a curve in the Lagrange Grassmannian) using the fact that any
segment of the V -geodesic is again a V -geodesic.
a one-parametric family of Lagrangian
subspaces (i.e. a curve in the Lagrange Grassmannian) using the fact that any
segment of the V -geodesic is again a V -geodesic.Then differential geometry of curves in the Lagrange Grassmannian provides basic differential invariants of V . The first coming ubiquitous invariants are the generalized Ricci curvature for parametrized curves and the degree 4 fundamental form for unparametrized ones. Among the realizations of the fundamental form are the constructed by E. Cartan invariant of rank 2 distributions in
 5 and a contraction of the Weyl tensor from conformal
geometry.
5 and a contraction of the Weyl tensor from conformal
geometry.
We are interested in Riemannian manifolds with constant scalar curvature admitting an infinitesimal non isometric conformal transformation. Ejiri [E] gave a negative answer to a conjecture in giving example of such manifolds but non isometric to the standard sphere. We propose to improve his study.
Vertex algebras (VA) give a rigorous mathematical definition of the chiral part of a 2-dimensional quantum field theory. It is an interesting problem, both from a mathematical and a physical point of view, to classify VA's which are generated by a Virasoro element L, a space g of even primary fields of conformal weight 1 (currents) and a space U of odd primary fields of conformal weight 3/2. I discuss a way to approach this problem and describe the solution in the case g is a simple Lie algebra and U an irreducible g-module. I will also show how, under certain assumption on the values of the Kac-Moody levels, one can prove transitivity of the group action on the sphere. This generalizes a similar result of Kac for the case of Lie conformal algebras.
For every bundle functor we introduce the concept of subordinated functor. Then we study subordinated functors for fiber preserving functors defined on the category of fibered manifolds with m-dimensional bases and fibered manifold morphisms with local diffeomorphisms as base maps. We also introduce the concept of the underlying functor and we show that there is an affine structure on fiber product preserving functors.
Let us have a convex domain in Euclidean plane. A billiard ball is a point that moves inside this domain along straight lines and rebounds from the boundary making an angle of incidence equal an angle of reflection. George Birkhoff considered the following question: How to estimate the number of closed billiard trajectories with a given number of rebounds? I deal with the generalization of Birkhoff's problem. I have found such esimates for the case of periods 2 and 3, a boundary is a manifold embedded in Euclidean space of arbitrary dimension. A definition of a generalized billiard trajectory is given.
It is demonstrated that higher reductions of the Dirac operator are closely related to projective-geometric aspects of line congruences in projective space.
Let P be a principal G-bundle over a n-manifold M, and C(P) its bundle of principal connections. For every Weil polynomial for G, f, of degree d, we have a canonically defined closed 2d-form in C(P). If 2d<=n it is well know that this form determines the usual characteristic class in M associated to f. If n<2d, we will associate to this form a (2d-n)-differential form in the space of connections in P, A. We will show that the equivariant cohomology classes determine equivariant extensions of this forms. As an application, we obtain canonical cohomology classes in the space A/Gau(P) of connections modulo Gauge transformations, and it is shown that they coincide with some classes previously defined by Atiyah and Singer. Finally we apply our results to the bundle of Riemannian metrics, and we show that, in the general case, the relevant cohomology is the equivariant cohomology of the corresponding variational bicomplex.
It is well known that natural operators of linear symmetric connections on manifolds and of classical tensor fields can be factorized through the curvature tensors, the tensor fields and their covariant differentials. We generalize this result for general linear connections on vector bundles. In this gauge-natural situation we need an auxiliary linear symmetric connection on the base manifold. We prove that natural operators defined on the spaces of general linear connections on vector bundles, on the spaces of linear symmetric connections on base manifolds and on certain tensor bundles can be factorized through the curvature tensors of linear and classical connections, the tensor fields and their covariant differentials with respect to both connections.
We will discuss deformation theory techniques for producing curves in principally polarized abelian varieties which are not jacobians. These techniques point to the possibility of producing curves of class (2g-6 choose g-3) times the minimal class in general principally polarized abelian varieties of dimension g. Up to now, the only class which is known to be representable by an algebraic curve in general principally polarized abelian varieties of arbitrary dimension g is (g-1)! times the minimal class: the class of a complete intersection of g-1 copies of the theta divisor.
We prove an analog of the Gauss-Bonnet formula for constructible sheaves on arbitrary reductive groups. This formula holds for all constructible sheaves equivariant under the adjoint action and expresses the Euler characteristic of a sheaf in terms of its characteristic cycle. As a corollary from this formula we get that if a perverse sheaf on a reductive group is equivariant under the adjoint action, then its Euler characteristic is nonnegative.
An exposition of the cohomological properties of the Leznov-Saveliev's two-dimensional Toda equations, associated with the semisimple Lie algebras, will be given. Starting from the exhaustive description of the Noether symmetries and conservation laws for the Toda equations, we build the continuum of the recursion operators, either local or nonlocal in total derivatives, for their symmetry algebras. The nonlocal terms of these recursions provide an abelian Noether symmetries subalgebra, which we regard as the hierarchy of the Drinfel'd-Sokolov equations, i.e., the potential modified KdV equation analogs associated with the initial Lie algebra. The evolution of the traceless energy-momentum tensor for the Toda fields is then defined by the KdV hierarchy related to the mKdV equations by the Miura transformations. Also, we reveal several properties of the bi-Hamiltonian structures for these equations, and, in particular, show that the higher potential KdV equations act as densities of the Hamiltonians for the potential modified and the modified KdV hierarchies.
We study locally conformal symplectic structure and their generalizations from the point of view of transitive Lie algebroids. To consider l.c.s. structures and their generalizations we use Lie algebroids with trivial adjoint Lie algebra bundle MxR and Mxg. We observe that important l.c.s's notions can be translated on the Lie algebroid's language. We generalize l.c.s. structures to g-l.c.s. structures in which we can consider an arbitrary finite dimensional Lie algebra g instead of the commutative Lie algebra R.
For PS-file of the full text see here.
- Participation cancelled - Title and abstract are reported here as a "web poster".
Global and local indices of isolated sets of singularities of sections of vector bundles over smooth manifolds with boundary .
For sections and for pairs of sections of vector bundles over smooth manifolds with boundary global and local indices of isolated sets of singularities are introduced. These indices are generalisations of Poincare - Kroneker index (rotation number) and Arnold boundary index. Constructions of the indices admit transfer to the infinite-dimensional setting. Applications to the problem of solvability of non-linear equations are obtained.
We describe all canonical tensor fields of type (1,1) (affinors) on the tangent bundle of a symplectic manifold.
Atiyah has given a path integral representation of the Index of the Dirac operator, which was intensively extended by Bismut. This is an integral of forms over the loop space. We give a meaning to this integral by doing a current theory on the loop space, which uses a mixture between the traditional tools of Hida Calculus and the tools of non-commutative differential geometry.
The relation between generalized Jacobi morphisms and generalized Bianchi identities for field theories is analyzed. Applications to the description of variational symmetries and superpotentials for Lagrangian field theories are given.
The talk is based on our papers (see xxx archive):
1. Affine Linking Numbers and Causality Relations for Wave Fronts, math.GT/0207219.
2. Affine Winding Numbers and Front Propagation, math.GT/0301117.
3. Toward the General Theory of Affine Linking Numbers, math.GT/0302295
and some new unpublished results.
Relation of the barycenter for probability measures on the boundary of noncompact symmetric spaces with the maximum likely hood estimator in statistics. Existence and uniqueness conditions for the barycenter. Construction of certain families of probability distributions generalizing Cauchy distributions via the theory of non-compact symmetric spaces.
Consider an analytic map from a neighborhood of 0 in a vector space to a Euclidean space. Suppose that this map takes all germs of vector lines at 0 to germs of circles. Such map is called rounding. Two roundings are equivalent if they take the same lines to the same circles. It turns out that any rounding whose differential at 0 has rank at least 2 is equivalent to a fractional quadratic rounding. The latter gives rise to a quadratic map between spheres. We give some interesting applications of this result including - a description of rectifiable bundles of circles in dimension 4 which is surprisingly different from the corresponding results in dimensions 2 (Khovanskii) and 3 (Izadi) due to quaternions, - a classification of all Kahler metrics in complex dimension 2 whose real geodesics are circles. - a geometric description of Clifford algebras representations as nonlinear projections taking lines to circles.
We introduce Edge ruled surface of the generalized time like ruled surface in Minkowski space R1n. Moreover, some theorems related with Edge ruled surface are given.
We consider infinitesimal deformations of some geometric magnitudes in a space LN of non-symmetric affine connection. We use four kinds of covariant derivatives to express deformations.
In this work we consider an application of geometry in the case of the construction of the gears. Programe packages Mathematica and SolidWorks are used. The result is implemented at programe package Multired.