Geometry of Differential Equations
Joseph KRASIL'SHCHIK
A program of the course at the 2-nd Italian Diffiety School,
(Forino, February - March, 1999)
and the 2-nd russian Diffiety School
(Pereslavl-Zalessky, January 26 - February 5, 1999)
If you have difficulties with HTML,
kindly use TeX, DVI or
PS-files
Smooth manifolds. Smooth locally trivial vector bundles. Sections.
The
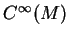 -module structure in
-module structure in
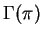 .
The jet
.
The jet ![$ [f]_x^k$](iskw99gif/img3.gif) of a local section
of a local section 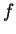 at a point
at a point 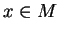 . The space
. The space
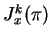 . Smooth structure in
. Smooth structure in
 . Manifolds
. Manifolds
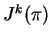 and bundles
and bundles
 . The jet modules
. The jet modules
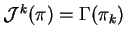 . Canonical coordinates
. Canonical coordinates
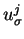 in
in 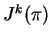 associated to a local trivialization in
associated to a local trivialization in  . Dimension of
. Dimension of 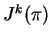 . The
bundles
. The
bundles
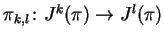 ,
, 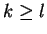 . Graphs of jets.
. Graphs of jets.
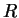 -planes. Presentation of points of
-planes. Presentation of points of 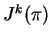 as pairs
as pairs
 , where
, where
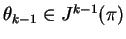 and
and
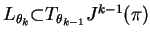 is an
is an 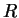 -plane.
Presentation of scalar operators as functions on
-plane.
Presentation of scalar operators as functions on 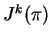 . Pull-backs
. Pull-backs
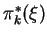 and nonlinear operators
and nonlinear operators
 as
sections of the bundles
as
sections of the bundles
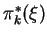 . Presentation of operators as
morphisms
. Presentation of operators as
morphisms
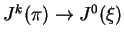 . The universal operator
. The universal operator
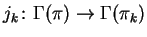 . Prolongations of nonlinear operators and their
correspondence to morphisms
. Prolongations of nonlinear operators and their
correspondence to morphisms
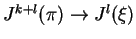 . Composition of
nonlinear operators.
Differential equations as submanifolds in
. Composition of
nonlinear operators.
Differential equations as submanifolds in
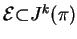 . Description
of equations by nonlinear operators. The first prolongation
. Description
of equations by nonlinear operators. The first prolongation
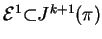 . Three definitions of the
. Three definitions of the  -the prolongation, there
equivalence. Solutions.
The Cartan plane
-the prolongation, there
equivalence. Solutions.
The Cartan plane
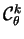 as the span of the set of
as the span of the set of 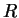 -planes at the
point
-planes at the
point
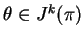 . The distribution
. The distribution
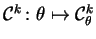 .
Description of
.
Description of
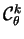 in the form
in the form
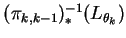 .
Local description of
.
Local description of
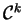 by the Cartan forms
by the Cartan forms
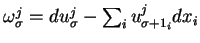 . A local basis in
. A local basis in
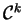 .
Involutive subspaces of the Cartan distribution. The theorem on maximal
integral manifolds. The type of a maximal integral manifold. Computation
of dimensions for maximal integral manifolds. Integral manifolds of
maximal dimension in inexceptional cases.
Lie transformations as diffeomorphisms of
.
Involutive subspaces of the Cartan distribution. The theorem on maximal
integral manifolds. The type of a maximal integral manifold. Computation
of dimensions for maximal integral manifolds. Integral manifolds of
maximal dimension in inexceptional cases.
Lie transformations as diffeomorphisms of 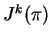 preserving the
Cartan distribution. Lifting of Lie transformations from
preserving the
Cartan distribution. Lifting of Lie transformations from 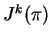 to
to
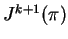 . The case
. The case 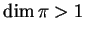 : correspondence between Lie
transformations and diffeomorphisms of
: correspondence between Lie
transformations and diffeomorphisms of 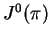 . The case
. The case 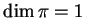 :
the contact structure in
:
the contact structure in  , correspondence between Lie
transformations and contact transformations of
, correspondence between Lie
transformations and contact transformations of  (inexceptional
case
(inexceptional
case
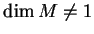 and exceptional case
and exceptional case 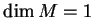 ). Local formulas for
liftings of Lie transformations.
Lie fields. Local lifting formulas. Global nature of lifting for Lie
fields. Infinitesimal analog for the Lie-Bäcklund theorem.
One-dimensional bundles. Generating functions of Lie fields. Correspondence
between functions on
). Local formulas for
liftings of Lie transformations.
Lie fields. Local lifting formulas. Global nature of lifting for Lie
fields. Infinitesimal analog for the Lie-Bäcklund theorem.
One-dimensional bundles. Generating functions of Lie fields. Correspondence
between functions on  and Lie fields for trivial one-dimensional
bundles. The jacobi bracket on
and Lie fields for trivial one-dimensional
bundles. The jacobi bracket on
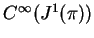 . Local coordinate
formulas for Lie fields and Jacobi brackets in terms of generating functions.
Bundles of higher dimensions. The element
. Local coordinate
formulas for Lie fields and Jacobi brackets in terms of generating functions.
Bundles of higher dimensions. The element
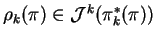 , its definition and properties. The Spencer complexes
, its definition and properties. The Spencer complexes
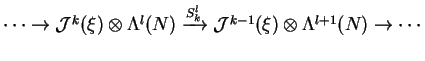 for a vector bundle
for a vector bundle
 , their
exactness. The element
, their
exactness. The element
 , its properties. Generating sections
, its properties. Generating sections
 as the result of construction of Lie fields with
as the result of construction of Lie fields with
 . Jacobi brackets for generating sections. Local coordinates.
Finite and infinitesimal symmetries, definitions. ``Physical meaning''
of generating functions. Determining equations for coordinate computations.
An example: symmetries of the Burgers equation
. Jacobi brackets for generating sections. Local coordinates.
Finite and infinitesimal symmetries, definitions. ``Physical meaning''
of generating functions. Determining equations for coordinate computations.
An example: symmetries of the Burgers equation
 .
The restriction
.
The restriction
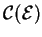 of the Cartan distribution to
of the Cartan distribution to
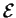 . Exterior
. Exterior
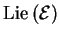 and
interior
and
interior
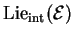 symmetries of an equation
symmetries of an equation
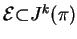 . The homomorphism
. The homomorphism
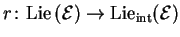 .
Counterexamples.
Algebraic model. The basic constructions. Cohomological invariants.
.
Counterexamples.
Algebraic model. The basic constructions. Cohomological invariants.
Questions and suggestions should go to
J. S. Krasil'shchik, josephk @ diffiety.ac.ru.
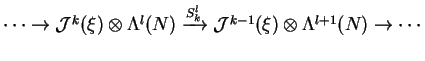 for a vector bundle
for a vector bundle