Algebraic theory of linear
differential operators and
introduction to geometry of jet spaces
Joseph KRASIL'SHCHIK
A program of the course at the 1st Italian Diffiety School
(Forino, July 17 - August 1, 1998)
and at the 1st Russian Diffiety School
(Pereslavl-Zalessky, January 26 - February 5, 1998)
If you have difficulties with HTML,
kindly use TeX, DVI or
PS-files
- 1.
- Rings. Rings with unit. Associative rings. Commutative rings. Fields.
Examples.
- 2.
- Homomorphisms of rings. Kernels and images. Epi-, mono-, and isomorphisms.
Algebras. Examples.
- 3.
- Ideals. Quotient rings. Prime and maximal ideals.
- 4.
- Modules. Generators. Submodules and quotient modules. Direct sums.
Examples.
- 5.
- Homomorphisms of modules. Kernels and images. Epi-, mono-, and isomorphisms.
Exact sequences. Compositions of homomorphisms. Commutative diagrams.
- 6.
- Homomorphisms of modules over commutative algebras. Bimodule structure.
- 7.
- Free and projective modules.
- 8.
- Tensor products. The tensor, symmetric and skew-symmetric algebras
of a module.
- 9.
- Categories and functors. Natural transformations of functors. Representable
functors and representative objects.

- 10.
- Vector fields on manifolds as derivations of
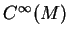 . The Leibniz rule.
. The Leibniz rule.
- 11.
- Derivations of commutative algebras. Module and Lie algebra structures.
- 12.
- Module-valued derivations. The modules
 . The commutator
identity
. The commutator
identity
![$ [a,[a',{\Delta}]]=0$](alg1_gif/img4.gif) . First order
differential operators
. First order
differential operators 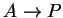 and their description.
and their description.
- 13.
- The algebraic definition of linear differential operators
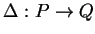 .
Equivalence of the algebraic and analytical definitions for the case
.
Equivalence of the algebraic and analytical definitions for the case
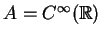 .
.
- 14.
- The bimodules
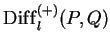 . The tautological operators
of order
. The tautological operators
of order 
 and
and
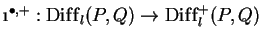 . The bimodule embeddings
. The bimodule embeddings
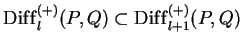 ,
the module
,
the module
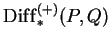 . The bimodules
. The bimodules
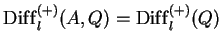 .
.
- 15.
- Composition of linear differential operators. The structure of an associative
algebra in
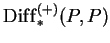 .
.
- 16.
- The exact sequences
and
The splitting
 .
.
- 17.
- The operators
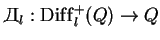 , their universal property. The
natural
isomorphism
, their universal property. The
natural
isomorphism
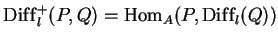 . Representability of
. Representability of
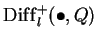 .
.
- 18.
- The universal composition
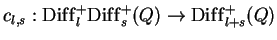 as a natural transformation of functors. Associativity of the universal
composition.
as a natural transformation of functors. Associativity of the universal
composition.

- 19.
- The submodules
 . The jet modules
. The jet modules
 . The operators
. The operators
 .
.
- 20.
- The universal property of operators
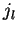 . The natural
isomorphism of
. The natural
isomorphism of 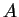 -modules
-modules
 .
Representability of
.
Representability of
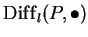 .
.
- 21.
- Functorial nature of
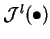 . The exact sequences
. The exact sequences
- 22.
- The module of infinite jets
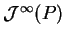 .
.
- 23.
- The universal cocomposition
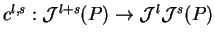 as a natural transformation of functors. Coassociativity of the universal
cocomposition.
as a natural transformation of functors. Coassociativity of the universal
cocomposition.
- 24.
- The embedding
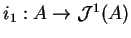 ,
,
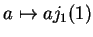 ,
, 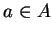 . The module
of
1-forms
. The module
of
1-forms
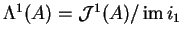 . The de Rham operator
. The de Rham operator
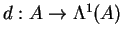 ,
,
 . The splitting
. The splitting
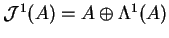 .
.
- 25.
- The universal property of
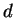 . The natural
isomorphism of
. The natural
isomorphism of 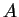 -modules
-modules
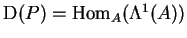 .
Representability of
.
Representability of
 .
.
- 26.
- Description of
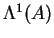 by generators and relations.
by generators and relations.
- 27.
- The modules
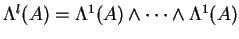 , the module
, the module
 .
Wedge product
.
Wedge product
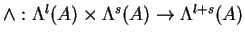 in
in
 .
.
- 28.
- The de Rham differential
 , its properties.
The de Rham complex and the de Rham cohomology.
, its properties.
The de Rham complex and the de Rham cohomology.
- 29.
- The Spencer jet complex
- 30.
- The modules
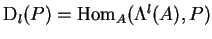 . The functors
. The functors
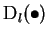 .
.
- 31.
- Elements of
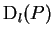 as skew-symmetric
as skew-symmetric  -valued multiderivations.
-valued multiderivations.
- 32.
- Wedge product
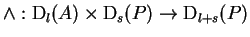 , its properties.
Structure of superalgebra in
, its properties.
Structure of superalgebra in
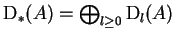 .
.
- 33.
- Inner product (contraction)
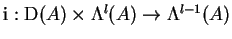 , its properties.
, its properties.
- 34.
- The formula
- 35.
- Action of derivations on differential forms (Lie derivative), its
properties.
- 36.
- The formula
- 37.
- Smooth algebras.
- 38.
- Motivations to consider fiber bundles: how to extend algebras of
observables? First examples: Cartesian products of manifolds, the
Moebius band, tangent and cotangent bundles.
- 39.
- Locally trivial fiber bundles. Morphisms. Sections. Subbundles.
- 40.
- Pull-backs. Restriction of a bundle to a submanifold. Whitney products.
- 41.
- Vector bundles. Morphisms. Kernels and images. Modules of sections, the
functor
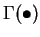 .
.
- 42.
- Direct sums and tensor products of vector bundles.
- 43.
- Evaluation of
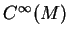 -modules at points of
-modules at points of 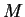 . Isomorphism between the
category of vector bundles over
. Isomorphism between the
category of vector bundles over 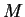 and the category of finitely generated
and the category of finitely generated
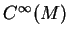 -modules.
-modules.

- 44.
- Example: evaluation of
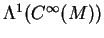 at points of
at points of 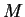 .
Ghosts. The geometrization functor
.
Ghosts. The geometrization functor
 and
geometrical modules. Geometrization of algebraic Calculus over
and
geometrical modules. Geometrization of algebraic Calculus over
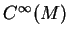 .
.
- 45.
- Evaluation of
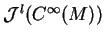 at point of
at point of 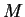 . Identification with
Taylor series of order
. Identification with
Taylor series of order  .
.
- 46.
- General geometric definition of the manifolds
 . Points of
. Points of
 as classes of tangent sections. Jets of sections. Local
coordinates.
as classes of tangent sections. Jets of sections. Local
coordinates.
- 47.
- Fiber bundles
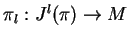 and
and
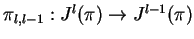 . Vector bundle structure in
. Vector bundle structure in 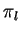 . Fibers of the bundles
. Fibers of the bundles
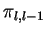 .
.
- 48.
- Scalar nonlinear differential operators as functions on
 .
General nonlinear differential operators
.
General nonlinear differential operators
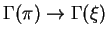 .
.
- 49.
- Nonlinear differential equations as submanifolds of
 .
Solutions.
.
Solutions.
- 50.
- How to diminish the order of a differential equation using the universal
cocomposition?
- 51.
- The Cartan distribution on
 , its maximal integral manifolds.
, its maximal integral manifolds.
- 52.
- Lie transformations and Lie fields. Symmetries.
- 53.
- Passing to infinity.
References
- M. F. Atiyah and I. G. MacDonald,
Introduction to commutative algebra, Addison--Wesley Publ. Comp.,
Reading, Massachusetts, 1969.
- S. Lang,
Algebra, Addison--Wesley Publ. Comp.,
Reading, Massachusetts, 1965.
- I. S. Krasil'shchik, V. V. Lychagin, and A. M. Vinogradov,
Geometry of jet spaces and nonlinear partial differential equations,
Gordon and Breach, New York, 1986.
-
I. S. Krasil'shchik, Calculus over commutative algebras:
A concise user guide, Acta
Appl. Math. 49 (1997), 235--248,
URL:
http://diffiety.ac.ru/preprint/96/01_96abs.htm.
-
Jet Nestrujev, Smooth manifolds and observables, IUM,
Moscow, 2000 (in Russian). English translation to appear.
Questions and suggestions should go to
J. S. Krasil'shchik, josephk @ diffiety.ac.ru.
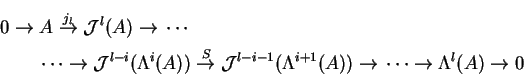
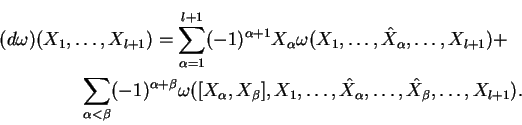
![$\displaystyle (\mathrm{L}_X{\omega})(X_1,\dots,X_l)=X{\omega}(X_1,\dots,X_l)-
\sum_{{\alpha}=1}^l{\omega}(X_1,\dots,[X,X_{\alpha}],\dots,X_l).$](alg1_gif/img58.gif)