Infinite Jets and Diffieties
Alexander Verbovetsky
A preliminary program of the course at the 5-th Italian Diffiety School,
(San Stefano del Sole, July 19-31, 2002)
Introduction.

I. Spaces of infinite jets.

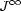
  1. The space J^\infty pi.
  2. Jets of submanifolds.
  3. Infinitely prolonged equations.

II-III. Basic differential geometric structures on infinite-dimensional manifolds.
  1. Smooth functions.
  2. Smooth mappigs, Lie transformations.
  3. Vector fields, Lie fields.
  4. Differential forms.

IV. Differential operators.
  1. Scalar and matrix differential operators.
  2. Prolongation of differential operators. One more example of a smooth mapping.
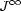
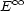V-VI. The Cartan distribution on J^\infty pi and E^\infty.
  1. Distributions on infinite-dimensional manifolds and their automorphisms.
  2. The Cartan connection.
  3. Maximal integral manifolds of the Cartan distribution.
  4. The structural element of an equation.
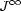
VII. Symmetries of the Cartan distribution on J^\infty pi.
  1. Generating sections of symmetries of the Cartan distribution on J^\infty pi.
  2. The structure of Sym (pi).
  3. Evolutionary derivations.
  4. The higher Jacobi bracket.
  5. Comparison with Lie fields.
VIII. Higher symmetries of differential equations.
  1. Exterior and interior higher symmetries.
  2. C-differential operators.
  3. Linearizations.
  4. Defining equations for higher symmetries.
IX. Examples of computations.
The exam has been passed by the following students:
  1. Luca Vitagliano (University of Roma)
  2. Gianni Manno (King's College London)
Questions and suggestions should go to school @ diffiety.ac.ru.