Authors: S. IGONIN, P. KERSTEN, I. KRASIL'SHCHIK

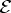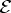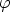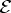
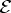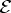We study the equation _fc of flat connections in a given fiber bundle and discover a specific geometric structure on this equation, which we call a flat representation. We generalize this notion to arbitrary PDE and prove that flat representations of an equation are in 1-1 correspondence with morphisms : _fc, and 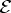_fc being treated as submanifolds of infinite jet spaces. We show that flat representations include several known types of zero-curvature formulations of PDEs. In particular, the Lax pairs of the self-dual Yang-Mills equations and their reductions are of this type. With each flat representation 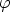we associate a complex C of vector-valued differential forms such that H¹(C ) describes infinitesimal deformations of the flat structure, which are responsible, in particular, for parameters in Baecklund transformations. In addition, each higher infinitesimal symmetry S of 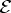defines a 1-cocycle c_S of C. Symmetries with exact c_S form a subalgebra reflecting some geometric properties of 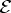and 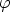. 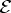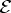We show that the complex corresponding to _fc itself is 0-acyclic and 1- acyclic (independently of the bundle topology), which means that higher symmetries of _fc are exhausted by generalized gauge ones, and compute the bracket on 0-cochains induced by commutation of symmetries.

24 pages, LaTeX-2e (AmSLaTeX) and diagrams.tex.

To compile source files (.tex) one needs the title page style files titlatex.tex.